TRADERS - Be(a)ware of diversification (part 1)

Published on Chartmill with kind permission of TRADERS’ Magazine. Check the original PDF article here

Spreading and its more sophisticated synonym ‘diversification’ is classically being heralded by the established financial industry as being the right, and for that matter the only, way to cope with risk. Nevertheless this is done with little to no nuance. All too often the disadvantages are underestimated, if mentioned at all. In this article series we’ll put on our analytical glasses to study the concept in depth to see if it’s such a great idea altogether. Of course, if it’s not, we must start wondering what better alternatives there are.

The idea to spread risk is an immediate consequence of evolution favouring the urge to gain and hold control over our environment and, more importantly to help achieve this, not taking any chances. In a physically hostile environment, the negative outcome might equal dying and hence not being able to procreate. We have the genetic makeup of those who ran and didn’t gamble. The ones who feared risk. Up to this day we’re stuck with this aversion to risk, as is well known since the field of behavioural finance saw the light of day. And this gets even more obvious if we mind historically shaped language constructs such as ‘not betting the farm’, ‘not putting all one’s eggs in one basket’ and ‘not betting all your money on one horse’.

Today, of course, our choices, specifically the ones we have to make in the stock market, don’t bring us those life or death effects anymore. There’s no reason to fear risk. Well perhaps there is, but far less than we subconsciously think. In fact risk equals opportunity, as without uncertainty financial markets wouldn’t exist in the first place. We merely should respect it and try to contain it. To put it in the words of Clint Eastwood: ‘if you want a guarantee, buy a toaster’. He would make one hell of a trader, I figure. Unfortunately nature didn’t reward thinking in probabilities.

To answer the question if diversification is an as good idea as being claimed, we’ll look into its origin and soundness as well as into the origin of profits. Because that’s why we take risk to begin with. As we’ll see, there’s a surprise there waiting for us.

Why do we spread?

Given the Darwinist motives above, let’s start by noticing that whenever spreading is mentioned, the spreading of risk is actually what’s being implicated. We spread risk! The general idea being that we somehow lower risk that way. And that’s for sure in almost all cases. To name one, think about the pooling of risk in the insurance industry. That’s a clear win-win situation. The insurance company gets paid a premium to divide a certain risk over a lot of people. Statistics tells us that we can’t even start to estimate the risk of one person having an accident, losing his house in a fire or dying before reaching a certain age. But we can fairly estimate the risk that a number of people will share such faith. As a matter of fact, the greater the number of people we monitor, the better we might estimate those odds. It’s the same situation we have with throwing up a coin. We can’t know for sure how many tails will emerge if we were to throw one coin up ten times once. There could be 0 tails as well as 10 tails, although we expect somewhere around 5. But if we do that say 10000 times, we’ll almost always get close to 5000 tails. Simply because the impact of each throw decreases as we increase the number of throws.

So, up to here, spreading seems to make a lot of sense. Let’s take this to the stock market. Does diversification lower risk? To answer that question we first have to ask another one.

What is risk?

This is quite a big question to ask. One that even academics haven’t settled on answering. For the most part risk is understood as the possible loss of your investment. But what if we make $100 in the stock market and subsequently lose it again. Is it a loss? To most it isn’t as long as it’s lost close enough in time to where they made it and preferably it’s lost while still being paper profit. That’s of course mental accounting rearing its ugly head.

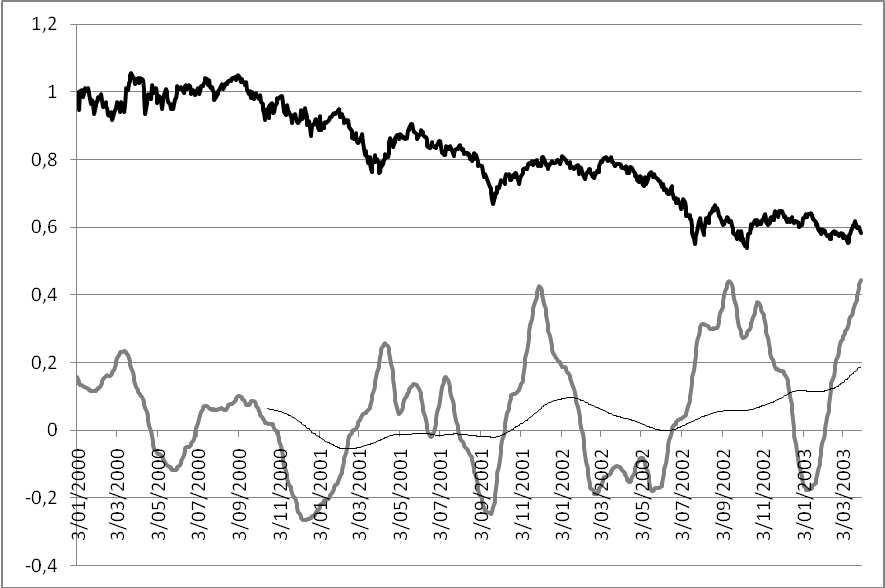
To stay on track here I’ll just stick to the difference between what’s called systematic risk or market risk and what is otherwise called unsystematic risk or idiosyncratic risk. The first being the risk that can be avoided by diversification, according to its Investopedia definition; The latter being the kind of risk that can’t be dealt with through diversification. There’s also systemic risk, the risk of a system meltdown leaving everybody with total loss. We won’t go into this type of risk. It’s quite remarkable that risk is defined along the terms of what diversification is able to do for us, because it makes it impossible to answer our question of what relation there is between risk and diversification. For instance, if an index goes down is generally considered market risk we can’t cope with through diversification. All boats are lift with the tide and vice versa everything outside gets wet when it starts raining. But what if a leader in a certain sector goes down because of idiosyncratic news relevant to only that leader, nevertheless dragging your stock down anyway. Is it systematic risk or idiosyncratic risk to your stock? More to the point, could it have been avoided with diversifying? Perhaps. Providing you diversified in non-correlated assets. To make things worse. Correlation isn’t constant. It seems to increase as stocks start trending either way as shown in the chart of figure 1.

To wrap things up diversification certainly does lower some idiosyncratic risk, even though it’s not clear to what extent nor to where idiosyncratic risk stops and systematic risk takes over. What’s more, in our insurance example, we’re not after profit. We just try to avoid risk. Now ask yourself, are you playing the stock market to win, or just to avoid losing? Let’s drag profits into our equation here, shall we?

What does diversification do with profits?

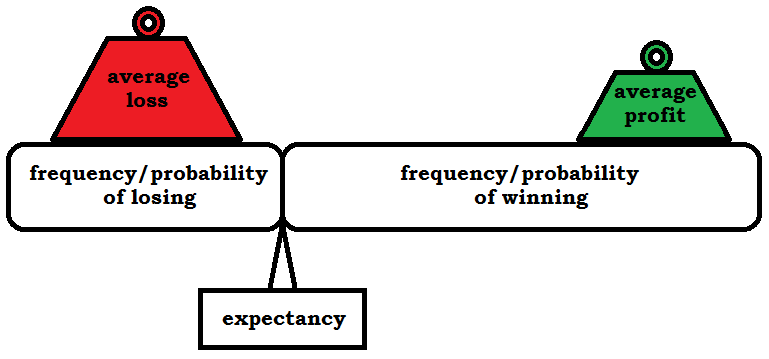
To that end we have to know where profit comes from. Average profit per trade can be written as being made up by four components in two dimension. On the one hand we have profitability given by the frequency of winning and losing. On the other hand there’s the average loss and average profit, accounting for what’s called the profit/loss ratio, giving the average amount of profit for each dollar we lose on average. The actual formula goes something like this:

The expected return in any probability game (as is trading), is given by the probability for a winner times the average profit for winners minus the probability of having a loser times the average loss for losers. Although quite some books put forward the argument that trading is about knowing your edge and the numbers to go with this formula, I don’t believe this to be true. We can’t know the future and any number we can obtain will only portrait history. These numbers are far from constant. But this doesn’t have to mean that the formula is worthless. What most authors are missing is the fact that this formula is about control. Getting the average return up can be done by increasing reliability. Doing all kinds of analysis to be right more often. But we happen to have far more control over our average loss and profit. If we would cut each loss at, say, 3%, our average loss could never become greater than 3%. We can do this just by selling, giving us ultimate control. Likewise we can add to our winners, protecting them without selling them. Given the representation in figure 2, successful trading is about manipulating the weights, not the scales. All successful traders and investors know this. Expectancy is the mathematical embodiment of ‘cutting loses and letting profits run’. In fact, it’s without doubt the main reason for their success if it’s not plain luck, as most of them freely admit ^(°). Given as few as 30% winners can earn one a fortune in the markets if only one knows how to handles winners and losers.

Funniest of all is that we avoid taking losses because we want to avoid them. We rationalize not taking them arming ourselves with shock logic. Selling our loses makes us admit we were wrong, turning a paper loss into a real one and selling with it all hope it will make up for it in the future. As if that’s not enough we sell our winners because we’re afraid they might turn into losers! We’re doing the exact opposite of what expectancy is telling us.

But with expectancy, we’ve arrived at the crossroads between risk, profit and diversification. For if it makes mathematical sense to accumulate winners and cut short losers, then overtime we should see our resources getting ever more concentrated in growing winners while losers are weeded out quickly. So expectancy is telling us not to diversify but concentrate our portfolio in the ones that proof to be winners. Here we have mathematical proof that diversification might be the bad thing to do. Especially because we live in a time were never before in history, we held more tools and products to sculpt our risk in the most meticulous ways we can imagine. We don’t have to estimate risk in some cases, we can actually define it beforehand. While diversifying, we seem to be trading to avoid losing rather than to try to win.

Next time

Could it be we’re on to something here? In the follow-up article we’ll run a true Monte Carlo experiment to see if returns are systematically better without diversifying, and if they are how we can systematically avoid diversifying safely. Stay tuned!

^(°) From acclaimed fundamental oriented investors like Buffett, Soros and Lynch to pure-sang traders like Minervini and his fellow interviewees in ‘Market Wizards’ and ‘New Market wizards’. I don’t even remember a single one not mentioning the importance of cutting losses and riding winners, as well as I hardly remember selection or timing being called of utter importance.

[FIGURE 1]

[HEAD] Correlation between stocks.

[CAPTION] Figure 1: Average correlation of a portfolio of stocks (grey) put up against the S&P500 (black) from 2000 until April of 2003. Correlation seems to have increased as the S&P500 came down from its top to its bottom given by the moving average on the chart.

[FIGURE 2]

[HEAD] Expectancy depicted as scales.

[CAPTION] Figure 2: Being profitable in the long run with trading, and all investing for that matter, is about cutting losses and letting profits run. Although it’s a hearsay thing of ages, statistical expectancy actually proofs the saying mathematical. It’s not about being right or wrong but handling both profits and losses well.